淺談解決問題的教學誤區和解決策略

瀘縣梁才學校 劉孝琴

“解決問題”是數學學習的重要內容，也是數學學習的重要目標。它不僅僅是解決一個或幾個問題本身，而是要讓學生經歷、探索、體驗和掌握解決問題的思想和方法。學生只有掌握了數學學習的解題思想和方法才掌握了數學學習的靈魂，只有掌握了解決實際問題的思想和方法，才能適應復雜多變的現代生活。解決問題如此重要，我們在教學中應避免哪些誤區呢？

一、“填鴨式”教學，教師直接告訴學生結論，忽視學生自主探索的學習過程。

部分教師認為沒有必要開展探究式教學，課堂教學只是讓學生掌握相關知識點，重要的是結果而不是過程。這樣學生直接根據教師教授的結論去解題，學生接受知識是被動的，容易造成對書本、教師權威的迷戀，缺乏探究和質疑意識。

二、只求創新，不重基礎性和時效性

所謂創新是在原有基礎上的創新，不能一味追求創新，忽視學生的基礎性及課堂的時效性。為了把課堂打造華麗生動，課堂上過分追求“情境創設、自主合作學習、解題方法多樣化”，結果課堂出現“自主表面化、合作形式化”的現象，形成教學的又一誤區。如教學周長的認識時，為了讓學生直觀感受到周長是圍成圖形一周的長，教師花了很多心思去制作秋天的場景，最后才出示小螞蟻沿著一片葉子爬行，進而引出周長的認識。其實只要出示小螞蟻沿著葉子爬行的畫面，引出對周長的認識就行了。

三、解決問題方法單一，學生發散思維受阻

傳統教學只要求學生把這道題解出來就行了，“還有其它的方法嗎？”這樣的問題很少有。而新課改提倡一題多解，只要學生言之有理，想出的辦法越多越好，而且特別重視打破傳統方法解題，再對多種方法進行優化比較。

四、前后知識脫節，知識不能融匯貫通

回顧教材，數學知識環環相扣，前后照應。在教學時，我們不能就本節課的知識而教學，應該多多復習相關知識，再把以前學過的知識和獲取的數學經驗遷移到本節課的學習中來。在不斷的復習舊知識與學習新知識的交融下，學生在“復習——學習——鞏固——再復習——再學習——再鞏固”的循環下，把知識融匯貫通。

五、就事論事，缺少深度、廣度和普及性

教學解決問題在于讓學生經歷探索解決問題的過程，積累經驗，掌握解題思想和解題方法，從而提高解決問題的能力。所以不能只停留在該題的解題方法上，還要進行歸類整理，由此題延伸到彼題，重解題思想和解題方法。

針對以上誤區，我們可以采取以下對策進行教學：

一、開展探究式教學，讓學生真正動起來。

開展探究式的學習，解決問題的過程就是“去探索、去發現，去創造”的探究過程。教師要借助學生身邊的豐富資源，創設生動活潑的生活情境，引導學生從情境中觀察、發現、收集數學信息，并進行篩選、提取，提出假想，再自主探究，驗證猜想、最后合作交流，反饋評價。

二、培養學生求異思維和優化意識

解決問題的教學目標在于開拓學生的解題思路，提高學生邏輯思維能力。要求一題多解不但能使學生舉一反三、觸類旁通，還能提高學生思維能力，社會優化意識逐步增強。

如教學：修一條水渠長100米，修這條水渠長的只用5天，照這樣計算，修完這條水渠還需幾天？

這是一道工程解決問題，學生很容易根據工程問題的數量關系，從不同的角度進行思考，得出算式：

（100-100x）÷(100x÷5)

100÷(100x÷5)-5

修這條水渠長的只用5天,可以把工作總量看作單位“1”列算式

可以轉化成按比例分配解決問題

(5÷1) x（4-1）

可以轉化成比例解決問題

可以轉化成倍數解決問題

可以轉化成方程解決問題

……

學生在解題后比較那種方法比較簡單，把知識進行整合，提高邏輯思維能力。

三、適時滲透數學思想和數學方法

數學思想和數學方法是解決問題關鍵所在，在教學上，我們要適時滲透相關的數學思想和數學方法。如轉化思想、類比歸納、類比聯想、數形結合、分類討論、換元法、假設法、對比分析等。這些方法的滲透可以讓學生掌握基本的解題思路，活躍思維，又能讓小學數學與初中數學接軌，避免把小學數學知識學得太死。如轉化法：教學比例應用題，讓學生轉化成分數應用題、按比例分配應用題、方程應用題、倍數應用題等；假設法：教學“一件衣服先上漲10%，又下降10%，現在的價格比原來的價格高還是低？”“甲比乙多5，丙比少乙7，甲和丙比較誰多誰少。”數形結合法：已知兩數之和為14，兩數之差為2，求這兩個數。 通過畫圖分析：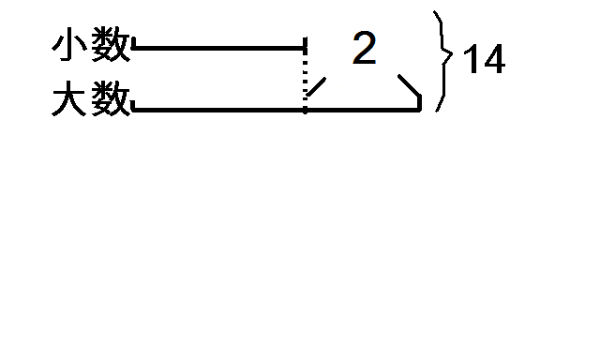

四、重視歸類和總結該類問題的解題方法

在教材中有很多的練習題，這些題看起來繁而雜，這就需要我們對這些習題進行歸類并總結解題方法。如五年級下冊教材的解決問題主要有：

1、長方體、正方體的表面積和體積計算。——根據公式，找相關數據，再按公式進行計算

2、分數應用題——總方法：(1)找單位“1”；(2)判斷已知或未知；（3）已知用乘法，未知用除法或列方程適用于六年級教材。五年級教材主要涉及到出現了兩個分率：用加法算一共幾分之幾；用減法算誰比誰多或少幾分之幾；用1減分率求還剩幾分之幾）。

3.方程應用題——根據等量關系解題，要求學生先找出等量關系再列方程

4.倍數應用題：——般設單位“1”為X，另一個表示出來。

5.相遇問題——抓等量關系：甲的路程+乙的路程=全程；（甲的速度+乙的速度）x時間=全程……

學生對解決問題進行歸類，解決問題變得簡單明了，掌握各類問題的解決方法，解題變得得心應手。

五、精講多練，但杜絕題海戰術

解決問題在于掌握方法，進行科學性練習。

1.對比練習。對于一些容易混淆的習題，需要進行對比性練習。如：用算術方法解題（1）甲40，甲比乙的3倍多10，求乙

(2) 甲40，乙比甲的3倍多10，求乙

第1小題，單位“1”未知，用除法，先加減數字，再除以倍數或分率，加減數字剛好相反。（40-10）÷3

第2小題，單位“1”已知，用乘法，按照順序列式計算。40 x3+10

2.經典題型練習。教師要對典型的題進行整理，讓學生經常練習，達到熟能生巧。

3.針對性練習。教師要及時檢查學生掌握習題的情況，對易錯易混淆的題進行針對性練習。

4.自我整理練習。（1）自編例題，鞏固新知識（2）錯題記錄，及時查漏補缺。（3）摘抄經典題型，經常練習。(4)自選作業，因材施教

六、數學回歸生活，學以致用

《數學課程標準》指出：數學要學以致用，要讓學生初步學會用所學數學知識和方法解決一些簡單的實際問題。如教學了“小數加減法”我們可以讓學生當“小小采購員”讓學生設計一個采購計劃：買什么物品，買多少才夠，每種物品的采價，做一個估算，然后再看一共要用多少錢，準備的錢夠不夠等等。在這一活動中，包含了很多的數學問題，學生可以積累很多的數學知識，感受數學知識對生活的改造，美化作用，還可以讓學生體驗到數學解決了生活實際問題的快樂。

總之，解決問題不僅僅是使學生學到知識，更重要的是使他們在錯綜復雜的情況中，利用所學的知識對具體問題作有條理的分析和預測，靈活而富有挑戰性的進行思考、探索，創造性地解決實際問題。